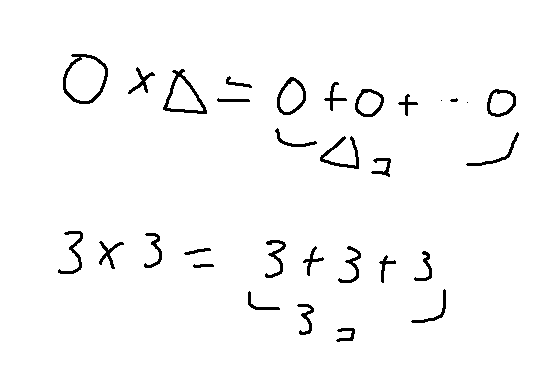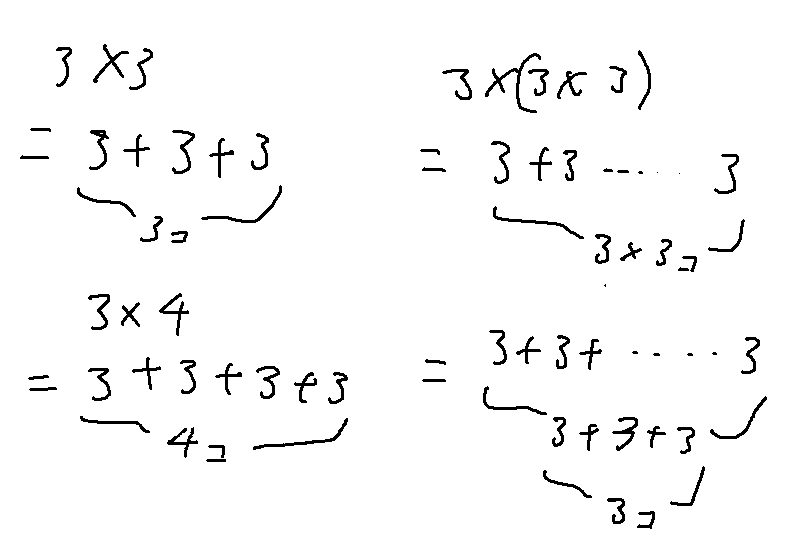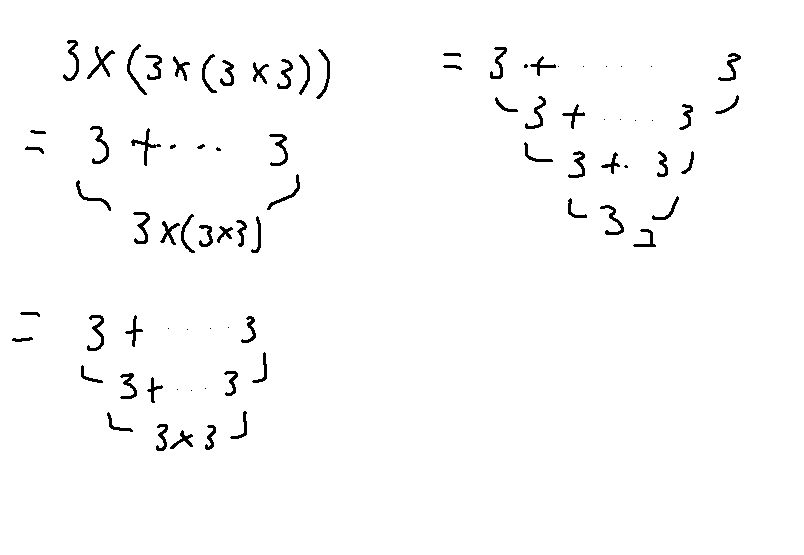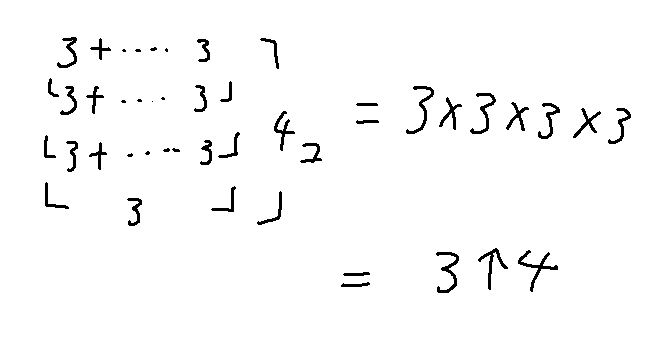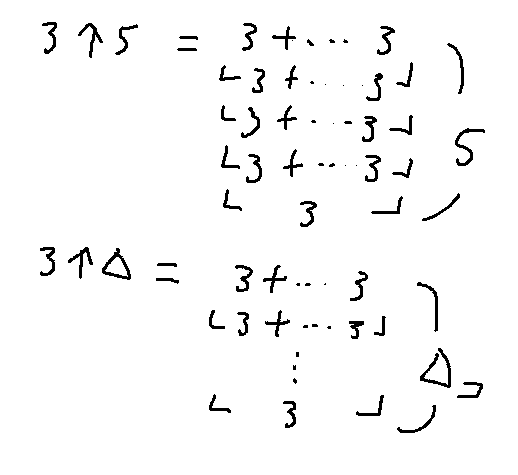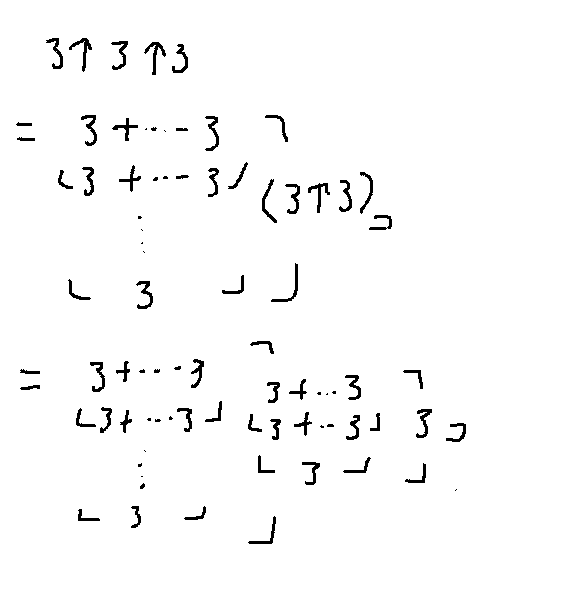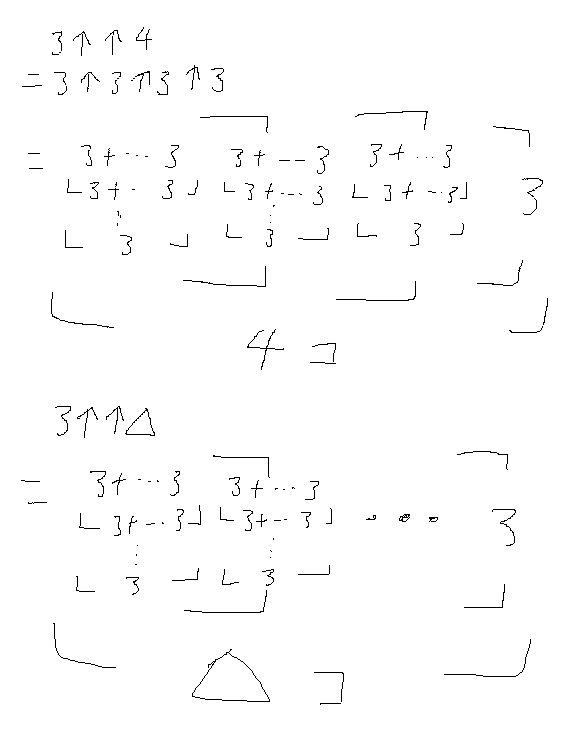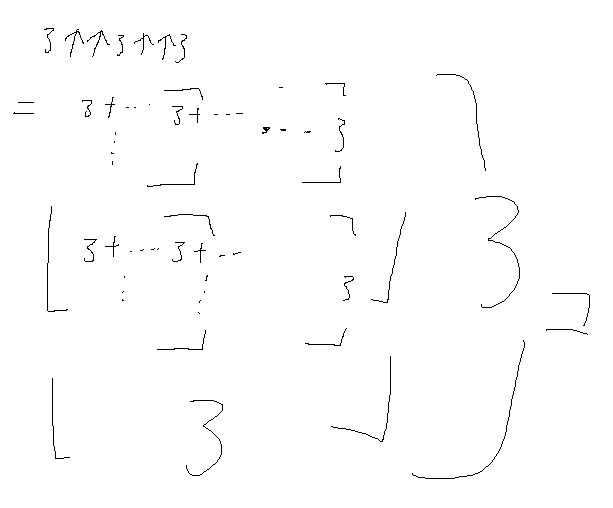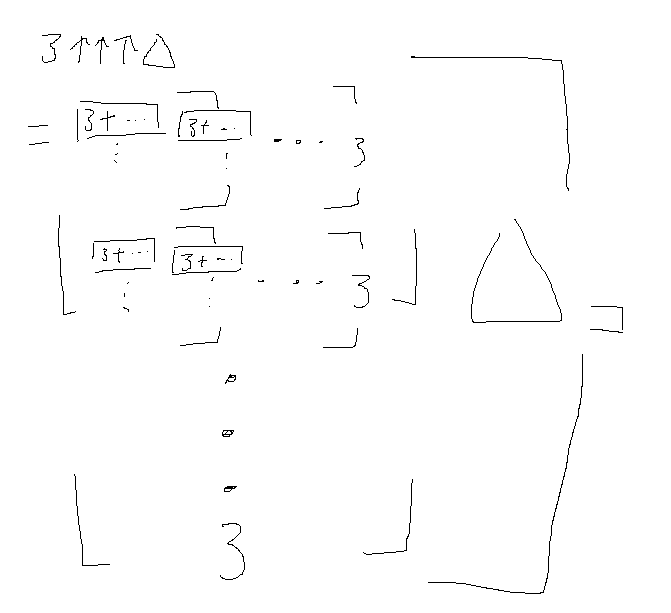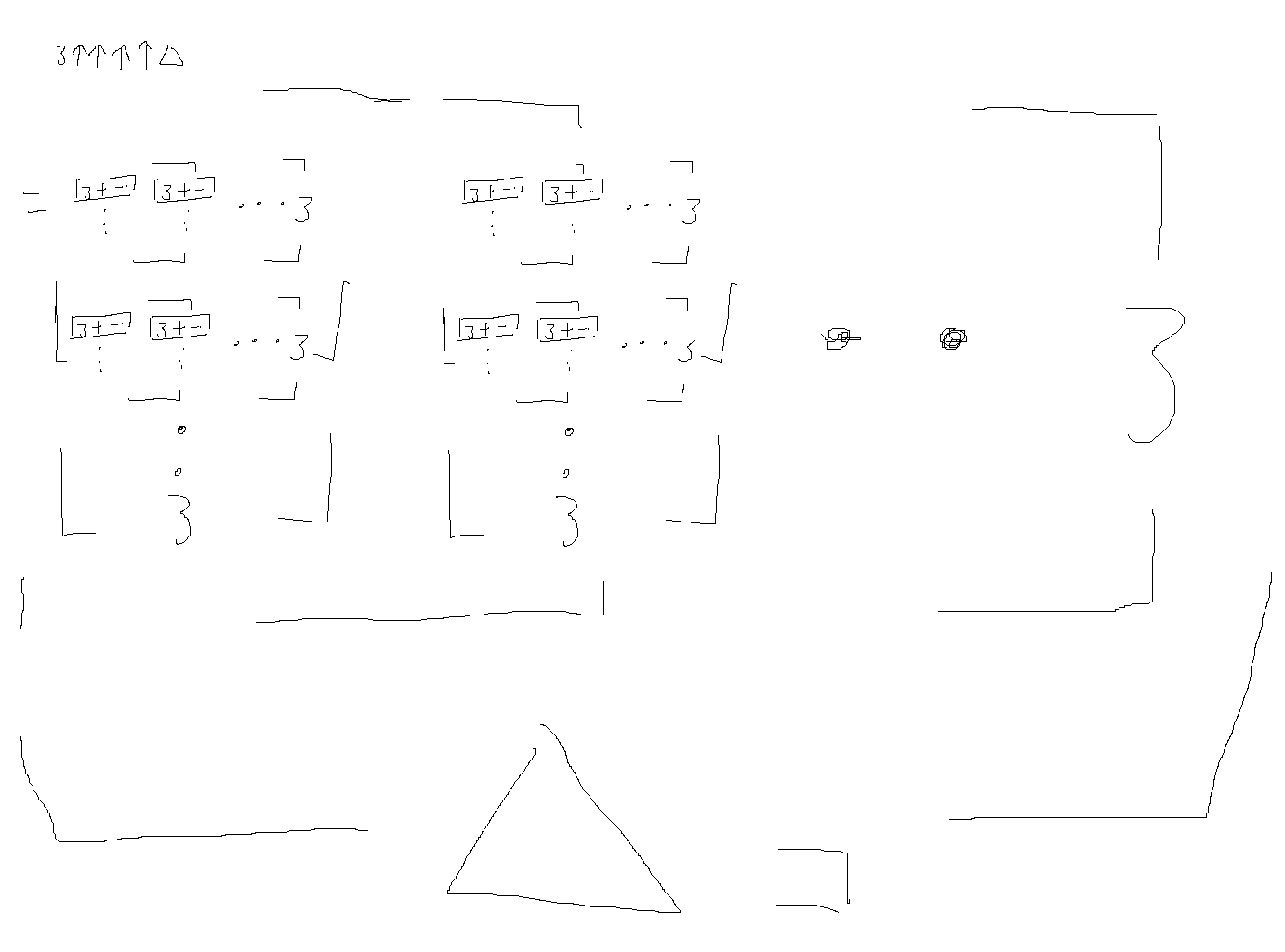LOCKYOUで学ぶ

矢印が増えるってどういうことよ？

戻る
ここまでテトレーション、ペンテーション、ヘキセーションとやってきたんだけど
矢印が増えていくと桁違いに数字が増えてくな
桁違いというか、桁の桁の桁の……っていう感じだね
今回は矢印が増えていくってどういうことかをちょっと整理するよ、いい？
へい構わねえ、殺すぞ
お笑いの言葉使えぃ！
えーっと、まずは
足し算 足し算の前にもう一つ演算が定義できたりしますが
めんどくさいのでなかったことにしてください
から始めていくね
これは普通にわかるな
3が3個だから、3×3
そこから右側の数を増やしていくと……？
3×4は3＋3＋3＋3
3×5は3＋3＋3＋3＋3
……これ延々とやってくのか？
そこらへんはまあ良いとして、
一気に飛んで3×（3×3）はどうなっちゃう？
3×（3×3）は、3×3は9だから……
ちょっと待って！！
！！
プレイバック！プレイバック！
なんなんだ？条件反射？
そこの3×3をあえて計算せずにそのまま書いてみよう
3×3を計算せずに……？
あーこういうこと？
そんな感じ
そんな感じで、次は3×3×3×3を書いてみよう
3×（3×（3×3））となって、3×3を計算せずに書くと……
法則が
見えてきた なんか180度回転させるとウン……
いや、なんでもない
ね
さて、×より一個上の記号は何だった？
累乗だな
3×3×3×3は3↑4だ
つまり、足し算の数が掛け算、足し算の積み重ねが累乗ってことになるね
図で書くとこんな感じだね
じゃあ次は3↑5はどんな感じになる？
積み重ねが一個増えるね
おんなじように3↑6なら6段、3↑7なら7段……
じゃあ、お次は3↑27行ってみよう！
27……は、3↑3だな
3↑3↑3となって……
今度は横に３段だね
ちょ～と大変なことになってきたね……
3↑3↑3↑3や3↑3↑3↑3↑3
つまり3↑↑4、3↑↑5とかのテトレーションは横に増えていくよ
お次は3↑↑（3↑↑3）、もう大体予想はつくよね？
まあ、こうなるから縦に重なるよな
ひどく雑になってます
ごめんね
ミルフィーユみたいだね
こうして考えるとペンテーション、ヘキセーションもどうなるかわかるよね
ペンテーションは累乗と同じ様になって縦に
ヘキセーションはまた横に……と
ペンテーションは潰れたミルフィーユみたいだね
それでヘキセーションは縦に潰れたものが横に潰れたミルフィーユみたいだね
その
ミルフィーユ縛り ……そもそもそんなにミルフィーユに似てるか？
はなんだよ
食いたいのか？
どっちかって言ったらミルクレープのほうが好きかなぁ
えーあたしはミルフィーユのほうが好きだな～
……
つまり、矢印が増えるごとに段の伸びが縦横2方向に増えていくんだな
指数とか底とかの
ただの数ひと 3↑↑↑3　＝　3↑↑？　＝　？↑↑3
と考えたとき、
3↑↑↑3
＝　3↑↑（3↑↑3）
≒　（（3↑↑（3↑↑3 － 2.5）））↑↑3
≒　（3↑↑3↑↑3）↑↑3　（大雑把に）
となります
驚きました
つ増やすより、矢印をひとつ増やしたほうが圧倒的に数が大きくなるね
縦が増えて横が増えて縦が増えて……っていうふうになっていっちゃうんだよね
あ、これまでの話をスライドショーにしてみたよ
これで今回の話の要点が大体つかめるかな？
テトレーションとかペンテーションとか、
数がものすごく大きくなる演算についていろいろやってきたんだけど
もとを辿れば普通の足し算になるんだよね
そりゃそうだけどさぁ
というわけど今回はここまで
次回はとうとうグラハム数についてやってくよ
お楽しみに～