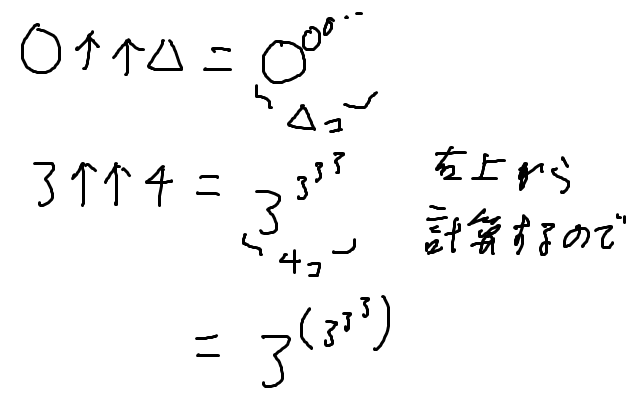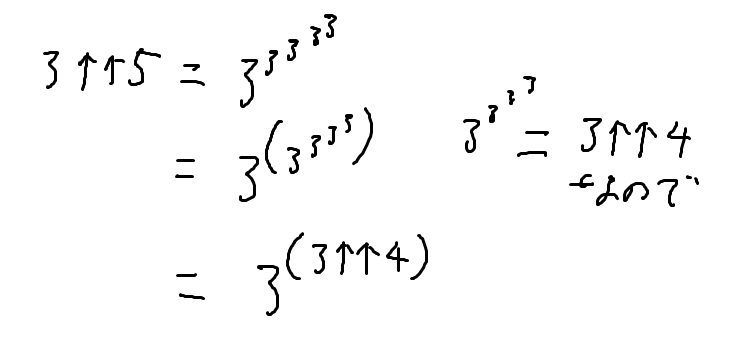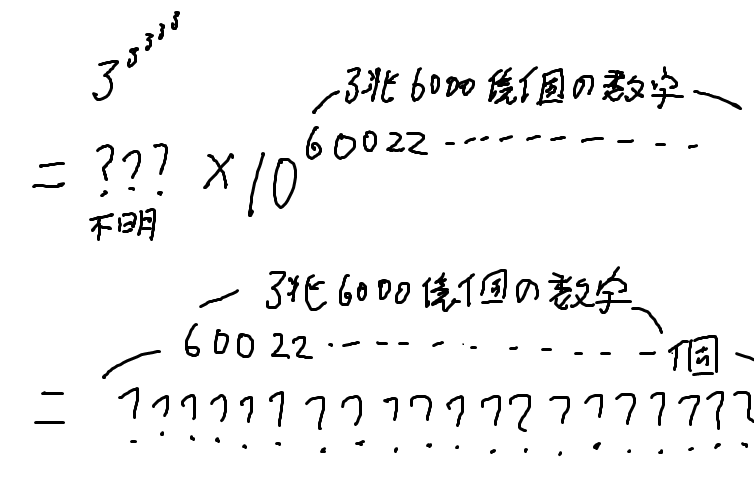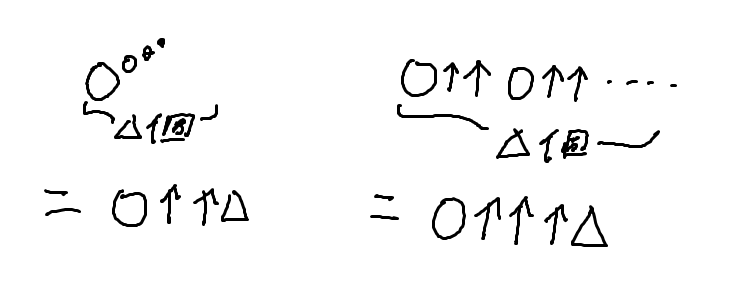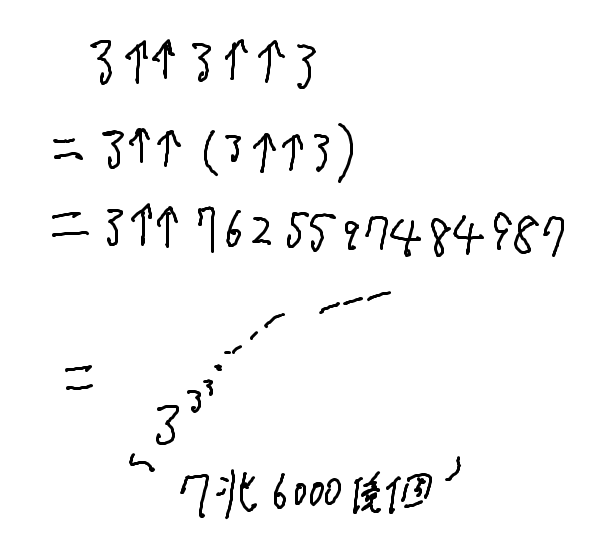前回は脱線した話だったけど
今回はグラハム数に近づくために更に上のステージに行くよ
今回はグラハム数に近づくために更に上のステージに行くよ
3↑↑↑3か?
テトレーションの上、ペンテーションだけど、その前にまずちょっとだけ
前回やったのは10↑↑3までで、
前回やったのは10↑↑3までで、
左側の数
 底(てい)と言います
底(てい)と言います
多分
は増やしたけど、多分
右の数
 指数と言……うんですかね?
指数と言……うんですかね?
a^bのbを冪指数って言うし、テトレーションを別名超冪って言うから
超冪指数になるのかな?
は増やさなかったよね
a^bのbを冪指数って言うし、テトレーションを別名超冪って言うから
超冪指数になるのかな?
そうだな
じゃあというわけで、3↑↑4を計算してみよう
うーん、3×3×3×3(3↑4)は9×9×9(9↑3)より小さいし、
9↑↑3よりは大きくならないでしょ(フラグ)
9↑↑3よりは大きくならないでしょ
実際に計算してみるね
まず、3↑↑4はこうなる
まず、3↑↑4はこうなる
3の上に3↑3↑3があるってことだよね?
指数の指数に指数がある状態だね
……ちょ、ちょっと待って!
……ちょ、ちょっと待って!
待たない
3↑3↑3は前に計算したよね?
3↑3↑3は前に計算したよね?
確か、7625597484987だったな
つまり3↑7625597484987ということになるな……
つまり3↑7625597484987ということになるな……
計算過程は前回のを見てもらうとして、
log(3)×7625597484987=3638334640024.0996855745793703822
つまり、1.258014290627491 × 10↑3638334640024
3兆6383億3464万0025桁だね
log(3)×7625597484987=3638334640024.0996855745793703822
つまり、1.258014290627491 × 10↑3638334640024
3兆6383億3464万0025桁だね
桁が3.6兆か……
9↑↑3は3.7億桁だから遥かに大きいな
9↑↑3は3.7億桁だから遥かに大きいな
ちなみにいま円周率は
今の時代でも
31兆4159億2653万5897桁
 2019年3月14日(円周率の日)に達成
2019年3月14日(円周率の日)に達成
桁数も3.1 4159 2653 5897と調整されてます
まで計算されてるから、桁数も3.1 4159 2653 5897と調整されてます
今の時代でも
計算自体は可能
 桁が一つ小さいのに加えて
桁が一つ小さいのに加えて
あっちは小数、こっちは整数なのでこっちのほうが遥かに楽だと思います
それでも結構時間かかると思うけどね
だと思うよ
あっちは小数、こっちは整数なのでこっちのほうが遥かに楽だと思います
それでも結構時間かかると思うけどね
誰が計算するんだ
それで4↑↑4は
4↑13407807929942597099574024998205846127479365820592393377
723561443721764030073546976801874298166903427690031858186486
050853753882811946569946433649006084096
4↑13407807929942597099574024998205846127479365820592393377
723561443721764030073546976801874298166903427690031858186486
050853753882811946569946433649006084096
ここまで来たら
桁数の桁数
 4↑↑4 =
4↑↑4 =
2.3610226715 × 10↑8 072 304 726 028 225 379 382 630 397 085 399 030 071 367 921 738 743 031 867 082 828 418 414 481 568 309 149 198 911 814 701 229 483 451 981 557 574 771 156 496 457 238 535 299 087 481 244 990 261 351 116
なので、桁数は
8 072 304 726 028 225 379 382 630 397 085 399 030 071 367 921 738 743 031 867 082 828 418 414 481 568 309 149 198 911 814 701 229 483 451 981 557 574 771 156 496 457 238 535 299 087 481 244 990 261 351 117桁になります、多分
ちなみに桁数の桁数は154桁
がわからなくなってくるな
2.3610226715 × 10↑8 072 304 726 028 225 379 382 630 397 085 399 030 071 367 921 738 743 031 867 082 828 418 414 481 568 309 149 198 911 814 701 229 483 451 981 557 574 771 156 496 457 238 535 299 087 481 244 990 261 351 116
なので、桁数は
8 072 304 726 028 225 379 382 630 397 085 399 030 071 367 921 738 743 031 867 082 828 418 414 481 568 309 149 198 911 814 701 229 483 451 981 557 574 771 156 496 457 238 535 299 087 481 244 990 261 351 117桁になります、多分
ちなみに桁数の桁数は154桁
ここからは先は左側の数を変えても大して意味がないから3固定で行くね
じゃあ、次は3↑↑5
じゃあ、次は3↑↑5
あかんもう勘弁して……
3↑↑5ということは3↑(3↑↑4)だね
これは……
つまり、3の上に3.6兆桁の数字が載っていることになるよ
おお、もう……
またまたおんなじように3↑↑5の桁数を調べようとしても
log(3)× (1.258014290627491×10↑3638334640024)
=6.0022×10↑3638334640023
log(3)× (1.258014290627491×10↑3638334640024)
=6.0022×10↑3638334640023
指数の小数部分がわからないから
先頭の数字
 末尾の数字は「7」
末尾の数字は「7」
3↑↑?は?が2以上なら全て末尾は7になります
すらわからんぞ
3↑↑?は?が2以上なら全て末尾は7になります
つまり3↑↑5はこういうこと……だよね?
そういうこと
恐ろしいぞ……
やってることは単純な足し算だよ?
そういう事言う……
3↑↑?の右側をどんどん増やしていけば、これまでよりも比べものにならないほど大きくなるんだけど
で、どれだけ増やせばグラハム数になるんだ?
いや、まだ特殊な操作が一個必要になるよ
その操作の説明のまえに3↑↑↑3の説明してないよね
前に大安がちらっと言ったと思うけど、おさらいも兼ねて改めて絵で説明するね
その操作の説明のまえに3↑↑↑3の説明してないよね
前に大安がちらっと言ったと思うけど、おさらいも兼ねて改めて絵で説明するね
この法則で言えば3↑↑3↑↑3が3↑↑↑3になるね
3↑↑3↑↑3↑↑3で3↑↑↑4
3↑↑3↑↑3↑↑3↑↑3で3↑↑↑5だね
3↑↑3↑↑3↑↑3で3↑↑↑4
3↑↑3↑↑3↑↑3↑↑3で3↑↑↑5だね
数字の増え方はこれまでと同じ法則だから簡単だよね
じゃあ、3↑↑↑3、つまり3↑↑3↑↑3はどのくらいの大きさになると思う?
じゃあ、3↑↑↑3、つまり3↑↑3↑↑3はどのくらいの大きさになると思う?
テトレーションも後ろから計算するんだろ?
つまり3↑↑(3↑↑3)
3↑↑3は……そうか、そうきたか
3↑↑3は……そうか、そうきたか
こうなるよね?
想像もつかん
次、3↑↑↑4はどうなると思う?
3↑↑3↑↑3↑↑3でしょ?
えーっと、まず右を計算して3↑↑(3が7兆個重なった数)
えーっと、まず右を計算して3↑↑(3が7兆個重なった数)
さっきの数分だけ3が重なった数か……
3↑↑↑5は?
問題の出し方がぶっきらぼうになってきてるぞ
なんも言えねぇ
と、いうわけで、矢印が3本のものはペンテーションって言うよ
さて、矢印が3本なら次は4本だね
さて、矢印が3本なら次は4本だね
名付けの法則からして次はヘキセーションか?
あったり~
3↑↑↑3↑↑↑3が3↑↑↑↑3になるよ
3↑↑↑3↑↑↑3が3↑↑↑↑3になるよ
うえっ
あ、言っとくけど3↑↑↑↑3がスタート地点だからね
あぁん!?なんで!?
その話はまたあとでやるとして、3↑↑↑↑3がどんな感じになるか
時間もないし次回説明しちゃうね
じゃあ、次もお楽しみにね~
時間もないし次回説明しちゃうね
じゃあ、次もお楽しみにね~