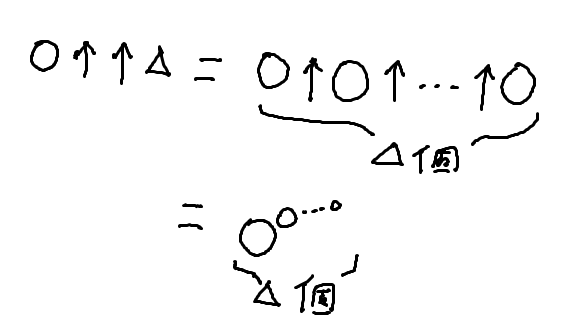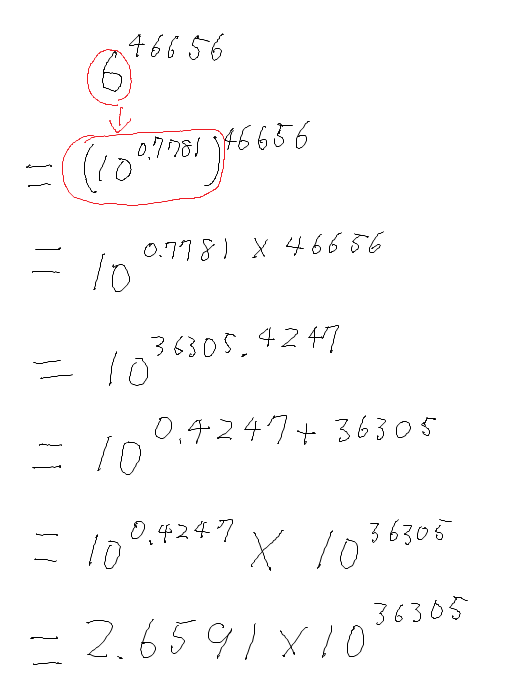前回は3↑↑3について話したいことがあるって行ったよね
ああ
↑↑って、テトレーションっていうんだけど、まあそんなことより
（名前ってかなり重要だと思うが）
テト……
「4」って意味？
テトラポッド
球体に４つの足がついた、コンクリート製の物体 海からの波を弱める働きをしています
ちなみに、テトラポッドは商標登録されています
とか
球体に４つの足がついた、コンクリート製の物体 海からの波を弱める働きをしていますちなみに、テトラポッドは商標登録されています
テトリス
例の全世界で人気な落ち物ゲーム 落ちてくるテトリミノが４つのブロックで構成されています
こちらも商標登録されているため、テトリスという名のついたゲームは許可なしに作ってはいけません
（非商用ならセーフ？）
とかあるけど
例の全世界で人気な落ち物ゲーム 落ちてくるテトリミノが４つのブロックで構成されていますこちらも商標登録されているため、テトリスという名のついたゲームは許可なしに作ってはいけません
（非商用ならセーフ？）
「4」って意味？
足し算、掛け算、冪乗とくるからね
それならなおさら前回僕が言った冪乗を「××」表記に……
というより足し算が1で「＋」なら掛け算は「＋＋」、冪乗は「＋＋＋」で、
テトレーションは「＋＋＋＋」って
4つだし
というより足し算が1で「＋」なら掛け算は「＋＋」、冪乗は「＋＋＋」で、
テトレーションは「＋＋＋＋」って
したほうが良かった
演算子＋や×を数字で表したハイパー演算子というものがあります
詳しくはまた今度
んじゃない？
演算子＋や×を数字で表したハイパー演算子というものがあります詳しくはまた今度
4つだし
冪乗までは普通によく使うから一つの記号で表すほうがいいけど
テトレーション以降はあんまり使わないからねぇ
それにグラハム数とかは↑を増やすのが前提で話が進んじゃってるからいまさら直せないよ
テトレーション以降はあんまり使わないからねぇ
それにグラハム数とかは↑を増やすのが前提で話が進んじゃってるからいまさら直せないよ
そういうもんなんだね
そういうもんなんだよ
そういうもんなのか
そういうもんなのよ
なんだこの中身のないやり取りは
それはそうと、○↑↑△は、○が△個指数に重なっているっていう意味だよね
こうだな
右から
この図を見るとちょっと嫌な予感がするけど、まあいいや
この図を見るとちょっと嫌な予感がするけど、まあいいや
確かに定義としては覚えたけど、まだ使いこなせてないよね
殆どアレなものを使いこなす必要あるかどうかがアレだけど
というわけでいくつか問題を出すよ
まず、3↑↑3が7.6兆ぐらいだったでしょ？
次は4↑↑3を求めよう
まず、3↑↑3が7.6兆ぐらいだったでしょ？
次は4↑↑3を求めよう
これは4↑4↑4だな
右側から計算するから4↑256
4の256乗だね
4の256乗だね
関数電卓使わにゃ大変だな
どうぞどうぞ
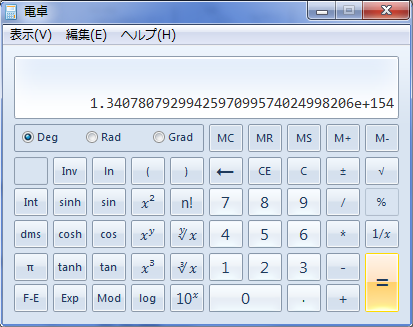
「4」「xy」「（」「4」「xy」「4」「）」「＝」で計算結果が出ます
答えは1.3407807929942597099574024998206e+154？
1.3408×10↑154だから、
1.3408×10↑154だから、
155桁
13 407 807 929 942 597 099 574 024 998 205 846 127 479 365 820 592 393 377 723 561 443 721 764 030 073 546 976 801 874 298 166 903 427 690 031 858 186 486 050 853 753 882 811 946 569 946 433 649 006 084 096
となります
？
13 407 807 929 942 597 099 574 024 998 205 846 127 479 365 820 592 393 377 723 561 443 721 764 030 073 546 976 801 874 298 166 903 427 690 031 858 186 486 050 853 753 882 811 946 569 946 433 649 006 084 096となります
3↑↑3が13桁だから、一気に増えたな
万、億、兆……の数の単位で一番大きい無量大数が68桁だからそれ以上だね
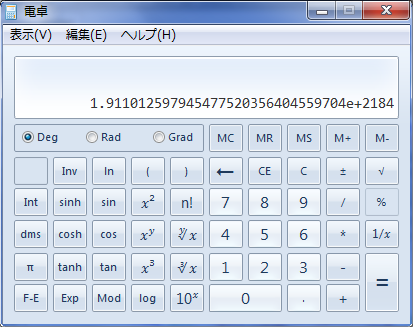
それで次は5↑↑3を計算してみて
それで次は5↑↑3を計算してみて
5↑3125＝1.911012597945477520356404559704e+2184
2185桁
19110125979454775203564045597039645991980810489900943371395127892465205302426158030120593865197398502655864401557944622353592127886738069722884101469159866020879618967571957018392816603380476112259755336261010014826511234131477682524114930944471769652827562851967375143953575424790932192066418830117871691225524210700507090646743828708514499502565861944615431835113798491336917799281274338404315492368555267835963741021053315460313537253257486369091597786903282664591829838152302869365728736914226481
31291743762136325730321645282979486862576245362218017673224940567642819360078720713837072355305446356153946401185348493792719514594505508232749221605848912910945189959948686199543147666938013037176163592594479746164220050885079469804487133205133160739134230540198872570038329801246050197013467397175909027389493923817315786996845899794781068042822436093783946335265422815704302832442385515082316490967285712171708123232790481817268327510112746782317410985888683708522000711733492253913322300756147180
42900752767779335230620061828601245525424306100689480544658470482065098266431936096038873625851074707434063628697657670269925864995355797631817390255089133122329474393034395616132833407283166349825814522686200430779908468810380418736832480090387359621291963360258312078167367374253332287929690720549059562140688882599124458184237959786347648431567376092362509037151179894142426227022006628648686786871018298087280256069310194928083082504419842479679205890881711232719230145558291674679519743054802640
46468540027339938607985944659615017525869658114475685100415686877309037124825353438392853975987494584970500382250124892840018265900562512861876299380444073401423470620557853053250349181895897071993056621885129631875017435359602822010382116160485451210393133122563322607664362366882968502088394961428304847391139916696226499485636852347128732947966808845094058939511046509441379095022765456531330186706335213230284605194343813998105614006525953007317907727110657834941746426847209561346473277485842382
74899668755052504394218232191357223054066715373374248543645663782045701654593218154053548393614250664498585403307466468541890148134347714650315037954175778622811776585876941680908203125になります
ツールチップに書くのは限界がありました
か、桁数の桁が増えてってるな
19110125979454775203564045597039645991980810489900943371395127892465205302426158030120593865197398502655864401557944622353592127886738069722884101469159866020879618967571957018392816603380476112259755336261010014826511234131477682524114930944471769652827562851967375143953575424790932192066418830117871691225524210700507090646743828708514499502565861944615431835113798491336917799281274338404315492368555267835963741021053315460313537253257486369091597786903282664591829838152302869365728736914226481
31291743762136325730321645282979486862576245362218017673224940567642819360078720713837072355305446356153946401185348493792719514594505508232749221605848912910945189959948686199543147666938013037176163592594479746164220050885079469804487133205133160739134230540198872570038329801246050197013467397175909027389493923817315786996845899794781068042822436093783946335265422815704302832442385515082316490967285712171708123232790481817268327510112746782317410985888683708522000711733492253913322300756147180
42900752767779335230620061828601245525424306100689480544658470482065098266431936096038873625851074707434063628697657670269925864995355797631817390255089133122329474393034395616132833407283166349825814522686200430779908468810380418736832480090387359621291963360258312078167367374253332287929690720549059562140688882599124458184237959786347648431567376092362509037151179894142426227022006628648686786871018298087280256069310194928083082504419842479679205890881711232719230145558291674679519743054802640
46468540027339938607985944659615017525869658114475685100415686877309037124825353438392853975987494584970500382250124892840018265900562512861876299380444073401423470620557853053250349181895897071993056621885129631875017435359602822010382116160485451210393133122563322607664362366882968502088394961428304847391139916696226499485636852347128732947966808845094058939511046509441379095022765456531330186706335213230284605194343813998105614006525953007317907727110657834941746426847209561346473277485842382
74899668755052504394218232191357223054066715373374248543645663782045701654593218154053548393614250664498585403307466468541890148134347714650315037954175778622811776585876941680908203125になりますツールチップに書くのは限界がありました
じゃあ次は……って言いたいところだけど
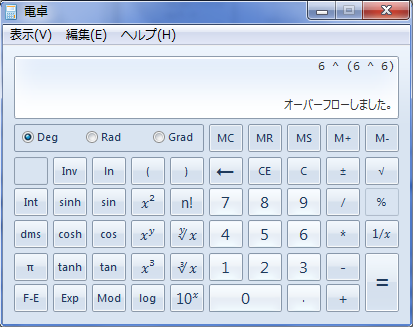
6↑↑3をやろうとしてもオーバーフローで計算ができないな
e+9999、つまり1万桁で限界になっちゃうみたいだね
おお でんたく
あふれてしまうとは なさけない...
あふれてしまうとは なさけない...
6↑6は46656だから10000桁以上になることは予想がつくよね
6↑46656をどうにかして10↑？？？の形にしたいということで、直接計算はせずに「log」をつかうよ
6↑46656をどうにかして10↑？？？の形にしたいということで、直接計算はせずに「log」をつかうよ
最初にやったあれか
まず、6をどうにかして10↑？？の形にする
つまり、10を何乗したら6になる？っていう問題を解くことになるよ
つまり、10を何乗したら6になる？っていう問題を解くことになるよ
まさしく対数の問題だな
これを数式で表すとlog10(6)ってなって、0.7781
つまり6＝10↑0.7781
これを数式で表すとlog10(6)ってなって、0.7781
つまり6＝10↑0.7781
だから、6を置き換えてこうなるね
(10↑0.7781)↑46656
(10↑0.7781)↑46656
カッコの中の指数と括弧の外の指数は指数法則で掛け算になるね
(10↑0.7781)↑46656 ＝10↑(0.7781×46656)
(10↑0.7781)↑46656 ＝10↑(0.7781×46656)
これは普通に計算できるな
(0.7781×46656)の答えは
36305.424737899277318329023726537
(0.7781×46656)の答えは
36305.424737899277318329023726537
10↑36305.424737899277318329023726537
で……大事なのは整数の方だから整数と小数を分けて
10↑（36305＋0.4247）
で……大事なのは整数の方だから整数と小数を分けて
10↑（36305＋0.4247）
指数の足し算は掛け算に変形できるから
10↑0.4247×10↑36305
＝2.6591×10↑36305
10↑0.4247×10↑36305
＝2.6591×10↑36305
36306桁
26591197721532267796......
って、ツールチップに書ききれるわけ無いだろっ
の数になるのか
26591197721532267796......って、ツールチップに書ききれるわけ無いだろっ
おんなじように7↑↑3から10↑↑3まで計算するとこうなるよ
7↑↑3 ＝ 3.7592×10↑695974 8↑↑3 ＝ 6.0145×10↑15151335 9↑↑3 ＝ 4.1821×10↑369693099 10↑↑3 ＝ 1.0000×10↑10000000000
円周率の諳記のギネスが7万桁ぐらい？
非公認でも10万桁だから6↑↑3が人間の記憶の限界かな？
非公認でも10万桁だから6↑↑3が人間の記憶の限界かな？
ここまで来たら実用的ではないな
とまあ、ここまでやってきたんだけど
テトレーションについてだいたいわかった？
テトレーションについてだいたいわかった？
ガッテン！
それで、次は何するんだ？
そうだね、テトレーションについてもうちょっとやったあと
次の段階へ進んでいっちゃうよ
今回はここまで！また次回！
次の段階へ進んでいっちゃうよ
今回はここまで！また次回！