LOCKYOUで学ぶ

グラハム数ってなんの数？

戻る
まあ大きい数の書き方はいいとして
それで本題のグラハム数ってやつだな
巨大数の代表として語られるものなんだけど、
そもそも何でこうして語られると思う？
確かギネス記録に載ったとか聞いたが
ただ、数字って無限にあるしな……そういや何でギネスになったんだ？
ざっくりいうと
「数学の証明で使われた最大の数」だからギネスに乗ったんだよね
単純に大きい数なら単純に＋１
すればいい 巨大な数のコンテストでは既存の数に＋１したり×2したり2乗したり……と際限がなくなるので
数の大きさではなく増え方の大きさを競います
だけだし
数学の何の証明で使われたんだ？
今回は「どんな数？」の前に
その部分「なんの数？」についてやっていきたいんだけど……
どうした？
よくわかんない 深い話になってくると
ラムゼー理論だの、グラフ云々だの……
そんなに難しいのか
まず、これを見てね

グラハム-ロトシルトの定理(1970)
n 次元超立方体の 2↑n 個の頂点のそれぞれを互いに全て線で結ぶ。
次に2つの色を用いて連結した線をいずれかの色に塗り分ける。
このとき n が十分大きければ、どんな塗り方をしても、
同一平面上にある四点でそれらを結ぶ線が全て同一の色であるものが存在する。

「グラハム-ロトシルトの定理」の名前はここのグラフ理論の深みを覗く　より
http://www.math.is.tohoku.ac.jp/~obata/activity/public.html
「グラハムの定理」でググったらなんか別のやつが出てきたので（よくわからん）
うーん……何だこりゃ
このとき n が十分大きければ、って書いてあるが
この定理の上限値がグラハム数って言うことか？
まず最初から説明するね～
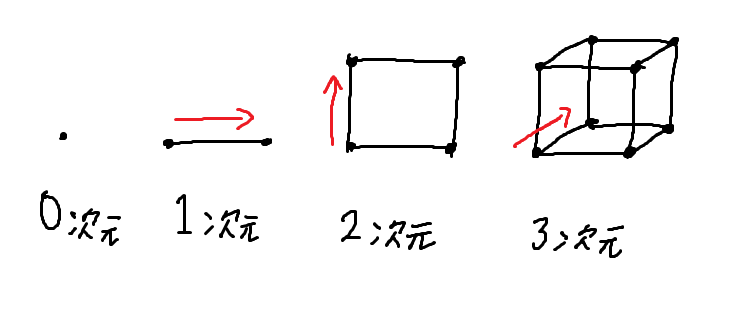
「n 次元超立方体」ってなんだか難しそうだけど、下の図を見てみて
点と線と、正方形、立方体の4つ
0～3次元のものか
3次元があるなら
4次元 この場合の4次元は縦横高さ×時間ではなく
縦横高さの線のいずれとも垂直に交わる線がもう一本ある次元のことをいいます
もあるよね、四次元ポケットとかよく聞くでしょ？
それで、同じ線をそれぞれの線と直角につなげたものがそれぞれの次元にあるなら、
4次元にも3次元立方体を超えた立方体「スーパー立方体」があるって思わない？
想像はできんが、たしかにそうかも……な？
それで4次元の超立方体があるなら5次元にも、6次元にも……
それらをひっくるめて「n 次元
超スーパー立方体 ちなみに超立方体は英語でhypercubeです
」になるよ
想像はできんが、まあそうだな……
次、2↑n 個の頂点
表記は変えてあるけどこれは「2のn乗」とおんなじ意味
1次元（線）なら2個の頂点、3次元なら8個の頂点ってことだろ
4次元なら16個か
次元の数の2乗の数だけ頂点がある……何で表記変えたんだ
それは後でのお楽しみ
サクサク進んでいくよ
頂点のそれぞれを互いに全て線で結ぶ
赤口、例として3次元立方体で描いてみて
わかった
どう色分けすれば分かりやすいんでしょうか……
自分で書いててなんだが、よくわからんことになった
線が
28本 頂点（8つ）から2つを選ぶ組み合わせ
8C2 ＝ (8×7)÷(2×1) ＝ 28
あっちゃうからねぇ
次に
2つの色を用いて連結した線をいずれかの色に塗り分ける。
適当に塗っていいんだよな？
赤と青で塗るぞ
これで最初の文章はわかったよね
次が問題の部分だけど
このとき n が十分大きければ、どんな塗り方をしても、
同一平面上にある四点でそれらを結ぶ線が全て同一の色であるものが存在する。
まず文の後半の
同一平面上にある四点でそれらを結ぶ線が全て同一の色であるものが存在する。
は、英語版wikipediaのグラハム数のページに乗ってた図をそのまま持ってくるね
これは左上の2つと右下の2つの4つの点を結ぶ正方形の線が
全部赤で成り立ってるんだな
でも、対角線のどっちかを青にしたら成り立たなくなっちゃうよね
だから、3次元ではそんな塗り方をしたら成り立たない
でも4次元なら、5次元ならっていう感じでやっていったら、いつかはどんな塗り方をしても全部赤か青の平面が出てくる
これが上に書いたグラハム-ロトシルトの定理ってやつだよ！
それで突き詰めていったら「グラハム数次元」なら
どんな塗り方をしても全部赤（もしくは青）の平面が出てくるって言うわけか
だいたいそんな感じ
なんかどれだけ増やしても成り立たないような気がするんだが、本当に成り立つのか？
いちおう成り立つことは証明されてるみたいだよ
今わかってる下限は13かな？前は6とか11とかだったけど
あと、最近研究されてきて、上限もグラハム数→小グラハム数→
ラブロスさんたちの考えた数 ラブロス数、っていう名前は特についてないみたいです

ってどんどん
減ってってきてる グラハム数と小グラハム数は世間に公表された順番は逆ですが

だから答えは13～ラブロスさんの数の範囲の中にあるよ　日進月歩っていうやつだね！
なんかなんて表現していいかわからんが、壮大だな
そうそう、ラブロス数と小グラハム数の間には大きな壁があるよ
それほどまでに大きさに差があるのか
いや、ラブロス数と小グラハム数の差より、
小グラハム数とグラハム数の差のほうが大きいよ
遥かに
じゃあ壁ってなんだ？
それはまた後でね
ちょっと具体的に言うと、計算方法かな
……まぁだいたいグラハム数が何の数字かはつかめた
よかった
それじゃあいよいよ本題の「グラハム数ってどんな数」をやっていくね
小休止
ちょっとおまけとして、上の色塗りを4次元の場合もやってみるけど、いい？
あんまりいい予感はしないが
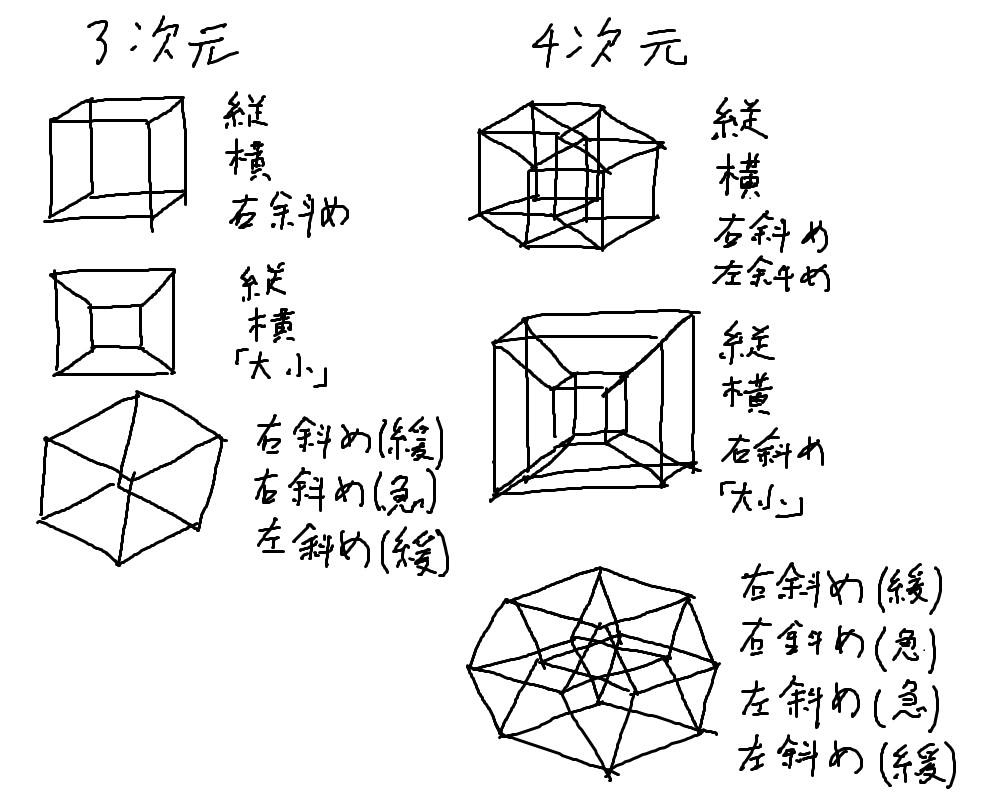
まず、4次元超立方体を図で描くと、こう！
右側に描いてあるものは「軸の向き」です
ただでさえややこしいんだから定規ツール使えよ……
そして、頂点を全部線で結ぶとこうなるよ！
ひとつ上の図の「右斜め（緩）右斜め（急）左斜め（急）左斜め（緩）」
のものの頂点をすべて線で結んだものになります
何なんだこれ
線の数は120本
めんどくさいから２色で塗るのは
無し 前後関係がややこしいから勘弁して……
だよ
あっそう
おまけはこれぐらいにしとこうね
おしまい！また次回！