LOCKYOUで学ぶ

指数と対数と指数表記

戻る
赤口、大きい数に興味はない？
ない
！！！
あーあー、聞いてやるよ
やった、じゃあ早速本題入っちゃうね
グラハム数ってあるよね？あれの説明したいんだけど
聞いたことはあるな
何にも例えられないぐらい大きいと聞いたが……
心配ご無用！
先は遠いけど千里の道も一歩からって言うしね
じゃあまず……ちょっとやっておきたいことがあるんだけど
例えば
1230000000 普通は三桁区切りにして1,230,000,000と表記します
何年経っても三桁区切りに僕は慣れません
っていう数字、パット見じゃわからないよね
一、十、百……１２億３千万か
たしかに分かりづらい
というわけで、こんな書き方をするよ 
1230000000 ＝ 1.23 × 100000000
           ＝ 1.23 × 108
具体的な細かい数字と、桁数とで分けて書く方法がある
コレを指数表記っていうんだけど
巨大数を説明する前に指数表記、さらに言えばそれを説明するために指数と対数についてやりたいと思ってるんだけどいい？
指数と対数は確か
数2 自然数の累乗は数1以前に習います
で習うやつだな
というわけで今から説明をしたいところなんだけど、作者いわくまだ話の構造がまとまってないから
完成までは申し訳程度のメモを代わりに貼っておくって
まとまってないならやるなよ……

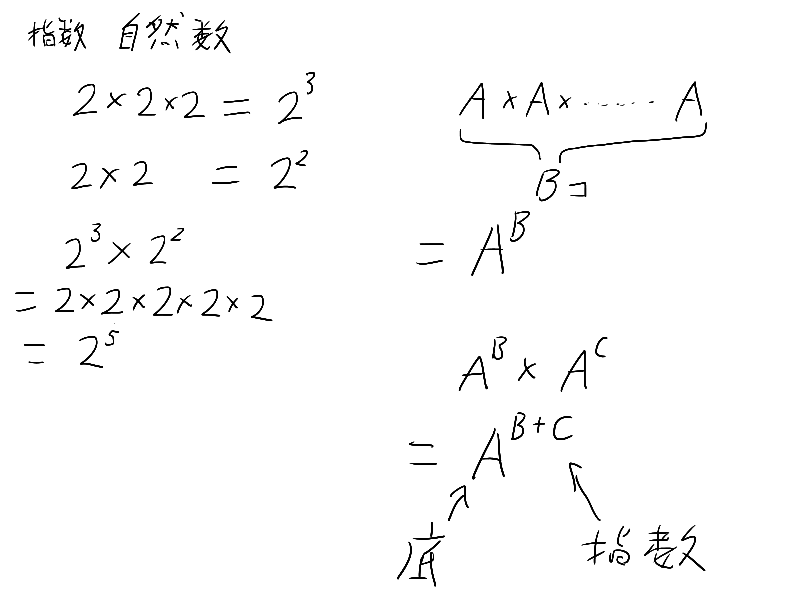
字が汚いな








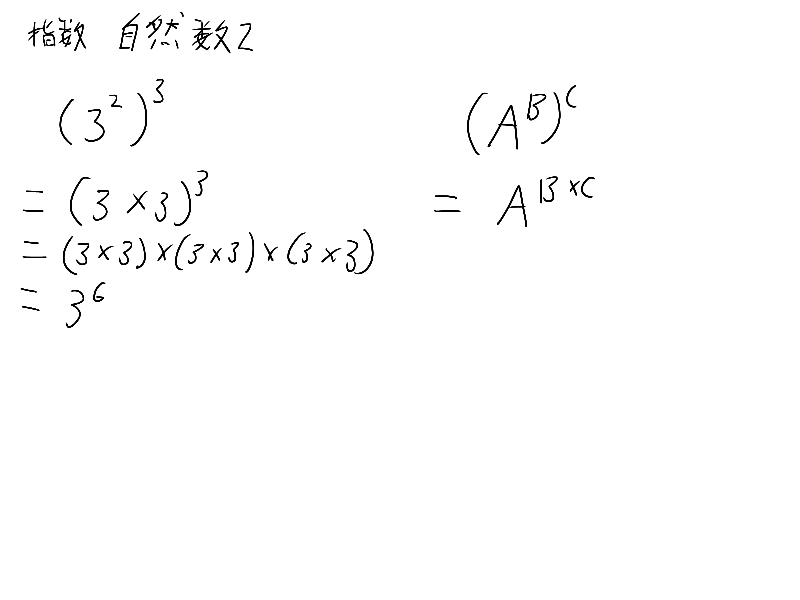
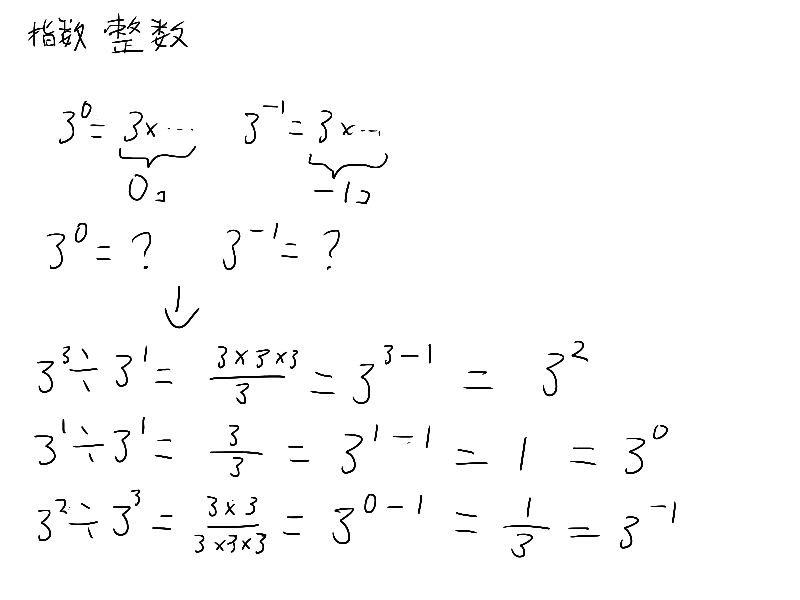
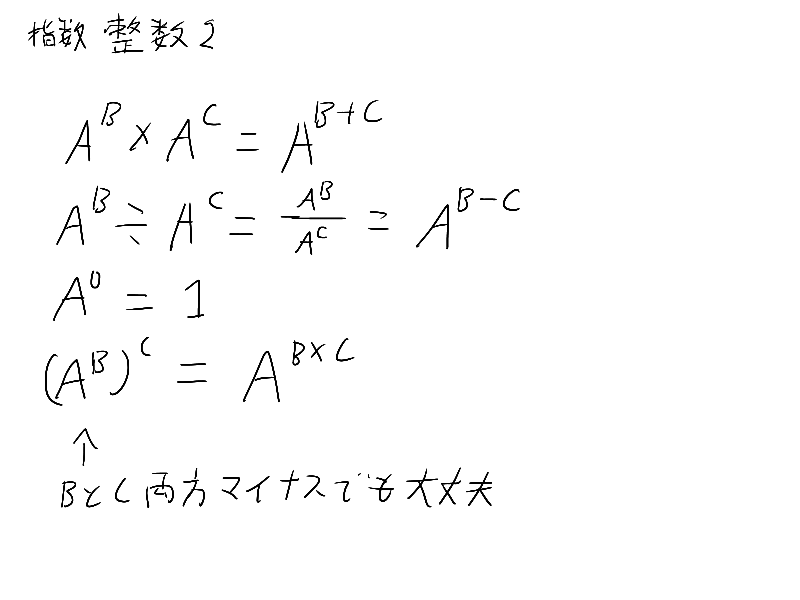
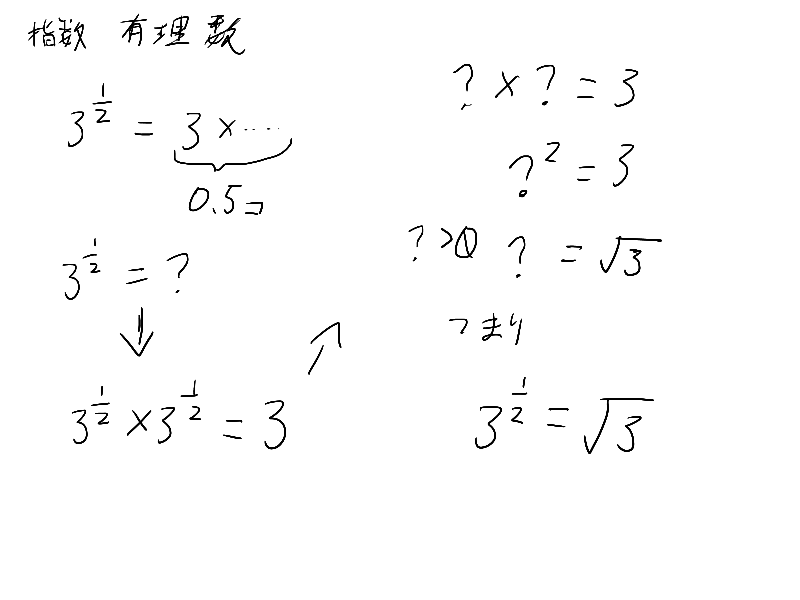
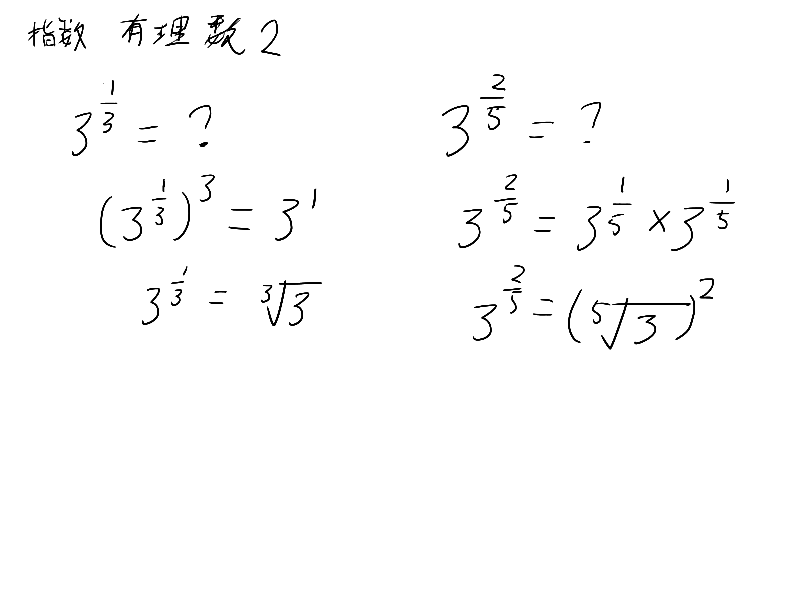
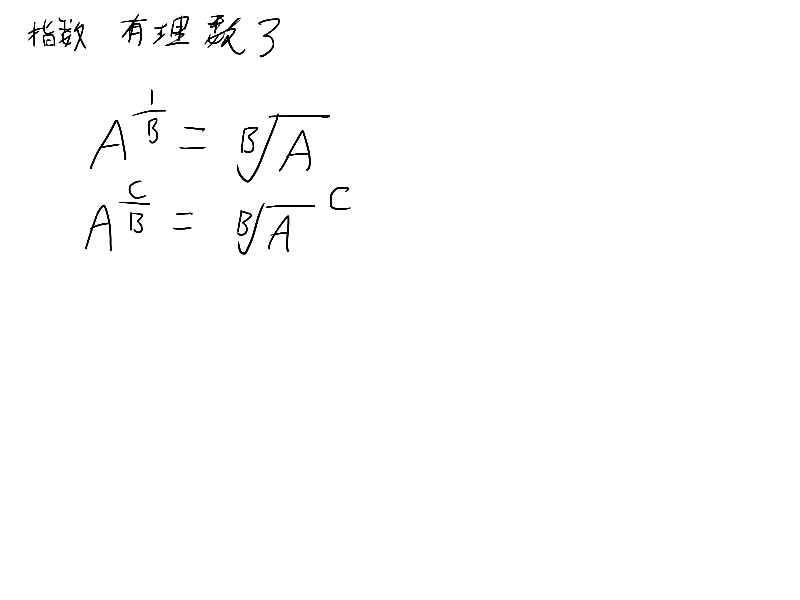
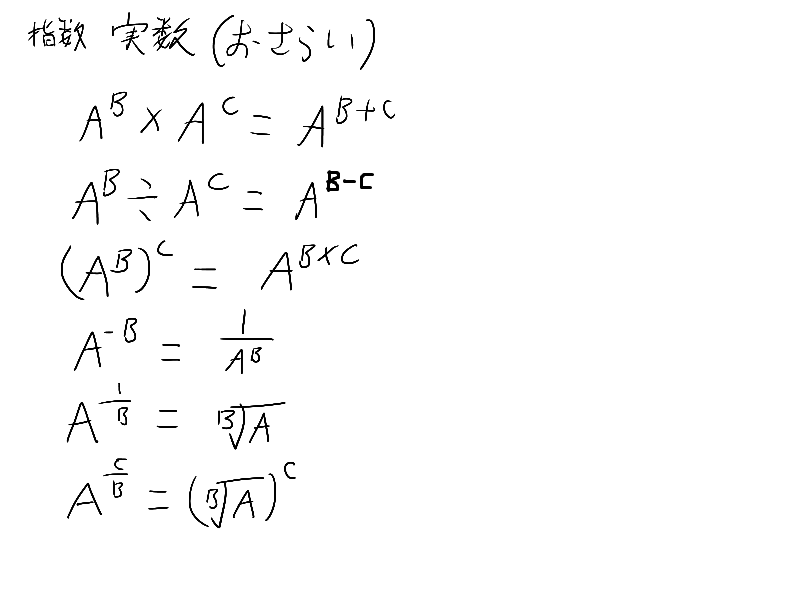
あ、ここの指数法則重要だから覚えておいてね

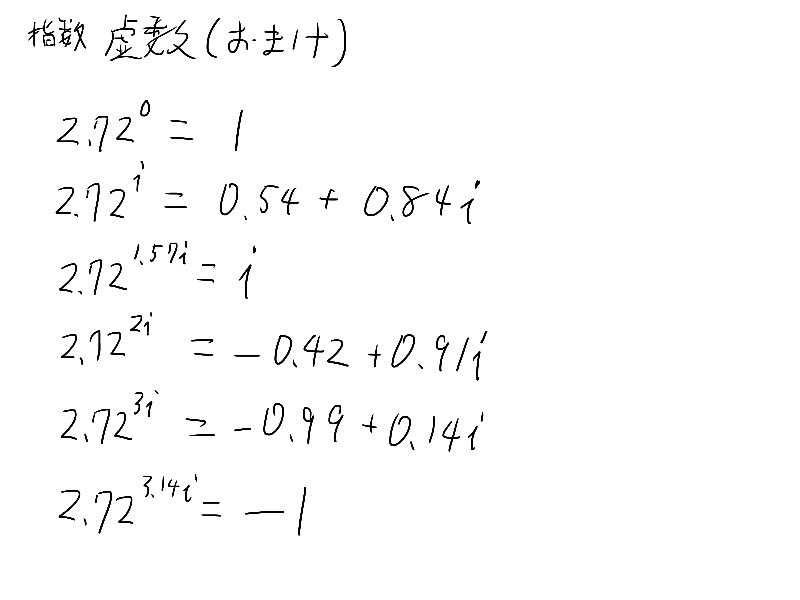
これ必要か？
wikipediaなんとなく漁ってたら面白かったから書いたんだって
あと
iのi乗 0.20788以外にも
111.31778、59609.7415、0.000388とかいろんな答えになります
よくわかんないですね
の答えは実数である0.20788、とかもなんか面白かったって
全く理解できないけど作者はこういうの読むの好きなんだって
そんなんだから行動が遅くなるんだろうが……

ここからは対数か

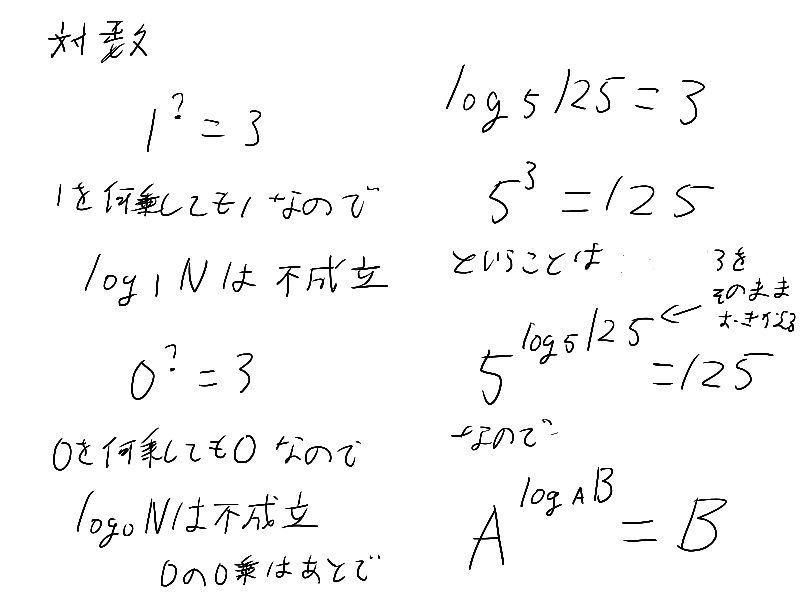
0の0乗は後でって書いてあるけど結局書くの忘れちゃったらしいからここで言っちゃうね
本当は定義できないけど大体の場合は1っていうふうになってるよ
ドナルド・クヌース 数学者、計算機科学者
アルゴリズムとかの研究をしているすごい人
もうちょっと後にも名前が出てきます
さんも1がいい！って言ってるしね








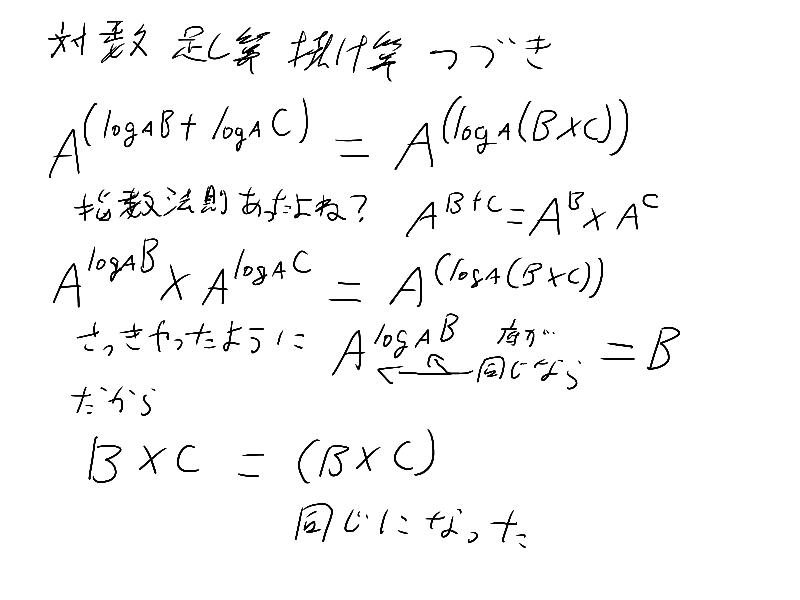
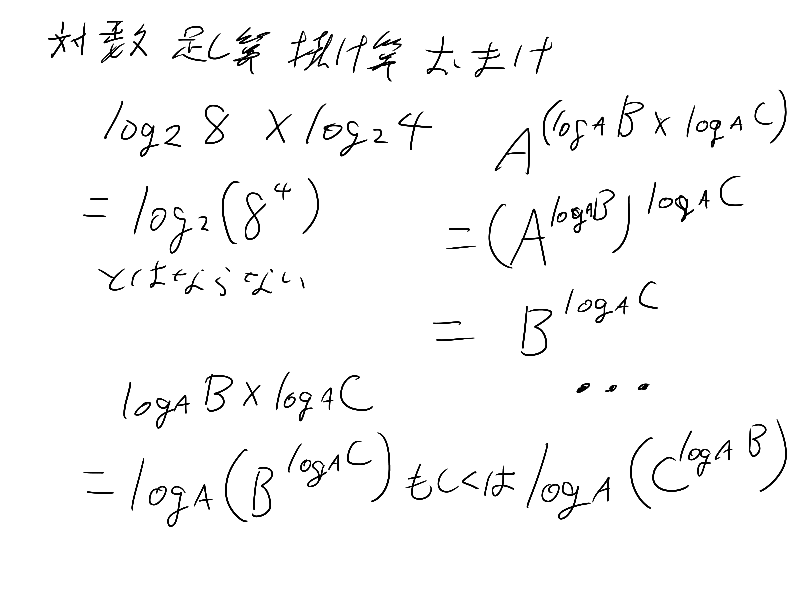
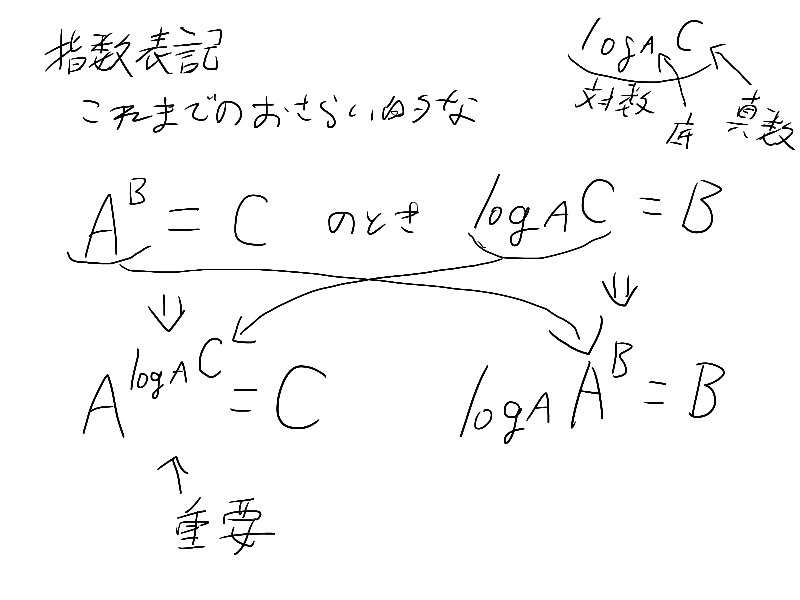
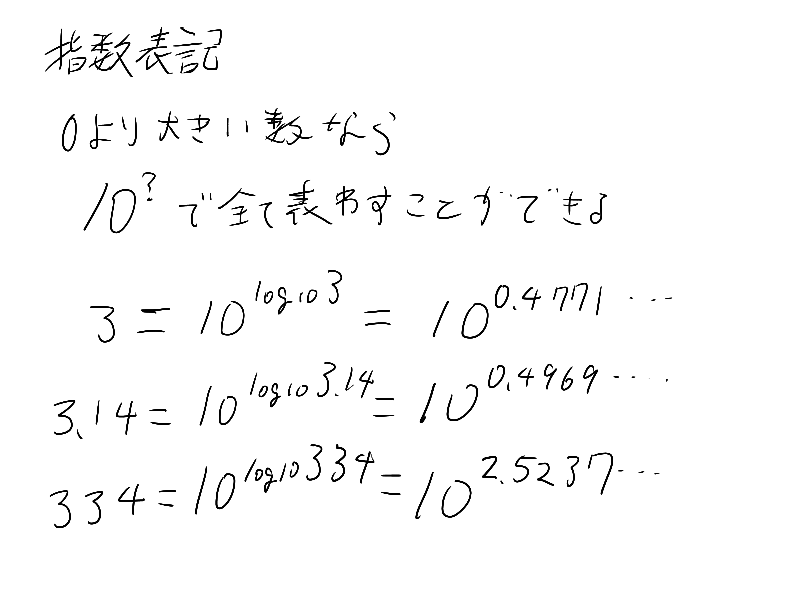
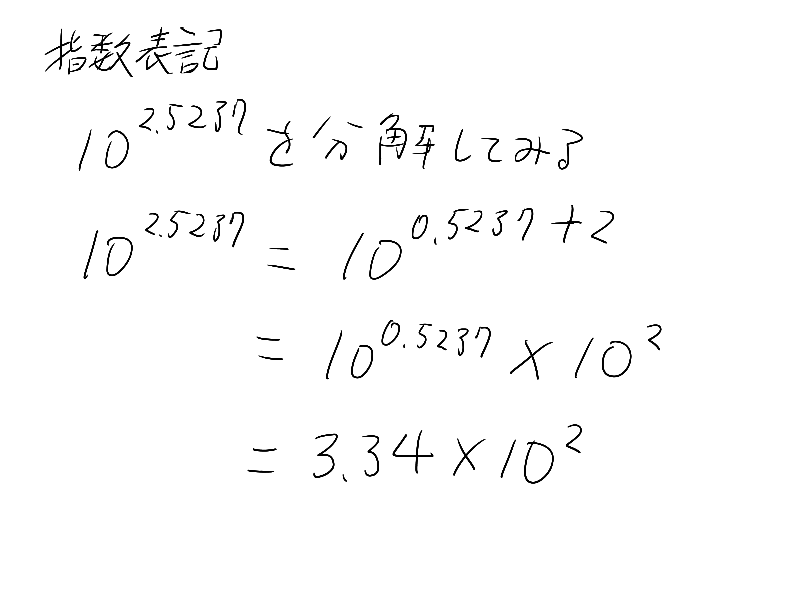
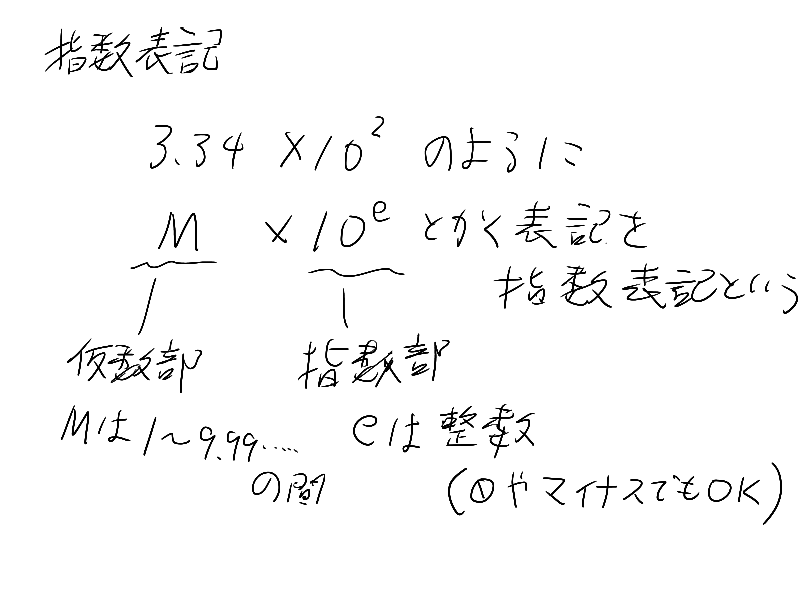
Mは1～9.999…の間って、10の0～0.999…乗とおんなじ意味だけど、大丈夫だよね？
まあここまでやってきたんだけどグラハム数ってそもそも指数じゃ到底表せないから
全くの無用の長物なんだよね
そんなに大きいのか……
じゃあ次はいよいよ本題のグラハム数に向けてやってくよ
次回もお楽しみにしちゃってね！