LOCKYOUで学ぶ

階乗進数

戻る
めええええええええええええええちゃあああああああああああああああんんんんんんん！！！！！！
……
もっふもっふもっふもっふｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ
ｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ
ｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ
ｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ
ｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ
（大安にまさぐられる）
よし！！！！階乗進法なんてどうでもいいからめぇちゃんをただもふもふするだけのコーナーにしよう！！！
大安あなた何を言ってるの？
ごめんごめん
めぇちゃん 大安が仏滅を呼ぶときの呼び名
たまに「めぃちゃん」という表記ゆれもするらしいが正直どうでもいい
1厘ぐらい冗談なんだけど
今回はちょっとした小話って言うことで、順列の順番について考えよう
この先作者が使うかもしれない～って言うことで
順列の順番ってどういうこと？
例えば、0,1,2,3,4の5つの数字があるとするでしょ
これを1列に並べる時、並べ方の総数はいくつある？
なんだか昔やったわね
5桁目が5通り、4桁目が4通り……ってなるから、5!＝5×4×3×2×1で120通りね
そだね
それじゃあ、並べ替えた結果の一個一個を昇順（小さい順）に並べ替えるとこうなるよね 
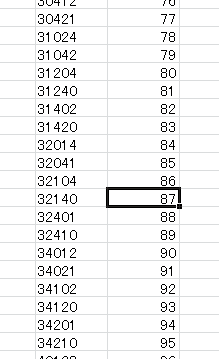
01234    0番目
01243    1番目
01324    2番目

...

43201    118番目
43210    119番目
あ、ちょっとこれから先都合のいいように、0番目から数えてるよ
順列の順番って、こういうことね
それじゃ一個問題、「32140」は何番目？
え？んーと……
こういうのを考えるのが今回の目的ね
ここを見てるみんなはスクロールする前にちょっと考えてみるのもいいかも？
なるほどねぇ
今回はここのサイトを参考にしてるよ
http://wasan.hatenablog.com/entry/2016/05/23/130403
http://wasan.hatenablog.com/entry/2016/06/02/134921
さて、さっきの答えなんだけど順番って言うことは要は前にいくつ数字があるかってことだよね？
そうね
数えるのが大変そうだけど
んじゃヒント
32140より前っていうんだから、0????と1????と2????の数字全部は絶対入ってるよね？
そうなるわね
0????って何個あるかわからないけど……あっ
0????って、1,2,3,4の順列じゃない
それだったら4×3×2×1で24個ね
……こういう考えでいいのよね？
大丈夫だっていけるいける！！
北京だって頑張ってるんだから！！
うるさいわね
それはともかく、1????と2????も同じ要領で考えられるから、24×3で72個でいいのよね？
正解＜エサクタ＞
……
次は30124から32140までの数字を考えればいいんでしょ？
だから30???と31???の数字は絶対入ってるから……
3×2×1＝6が2つ分あって、12個
ここまでで84個ね
更に続けると、320??で、2×1＝2が1つ分で2個
3210?と3211?……って数字は重複しないんだっけ、3210?だけでいいからこれで1個
合計で87個だから87番目ね
画像見てもらうと分かる通り、87番目で合ってるね
褒美としてオプーナを買う権利をあげよう
エクセルでこの表作るの地味に苦労しました
Wii持ってないわよ
それじゃあ、次はもっと汎用的に考えれるようにしよう
どんな順列が来ても同じように考えられるといいようにしようね
まあそうね
とりあえず最初から考えてみよう
まず最終的にはこういう計算式で個数を出したよね
統一感を出すように最後のやつにも1!をかけるようにするよ
3×4!＋2×3!＋1×2!＋1×1!
……なんか法則が見えそうで見えないわね
調べたい順列が32140だからそのまま数字×(桁目－1)!かければいいと思ったけど
2桁目の4のところは1だし……
さっきちょっと躓きそうになったよね？
そうね、普通に考えると
3210?と3211?と3212?と3213?の4つで、1,2,3は重複してるから数えないようにしたのよね
そうなると……自分の数字より小さい数があると駄目ってことでしょ？
ええぞ！ええぞ！
……ここが鍵になりそうね
ええっと、2桁目の「4」の前に「4」より小さい数は3つあるから4－3で1……って言うことでいいのよね？
最後の1桁目の「0」は……特に考えなくてもいいのね 
3     2     1     4     0
0     0     0     3     _
3*4!  2*3!  1*2!  1*1!
上段：順列
中段：前にある自分より小さい数値の数
下段：自分から自分より小さい数値の数を引いたものを階乗とかけたもの
そんじゃ、それを踏まえてもう一問
「40312」
えーと、並べて書くとこうなるわね
96+0+4+0
で100番目ね 
4     0     3     1     2
0     0     1     1     _
4*4!  0*3!  2*2!  0*1!
ナイスでーす！
……これでいいの？
やっぱり最後の数字が気になるんだけど
まあ、無理やり書いてみればいいんじゃない
そうね
……あ、絶対に0になるのね 
4     0     3     1     2
0     0     1     1     2
4*4!  0*3!  2*2!  0*1!  0*0!
そういうこと
んじゃ要領わかってきたところで、順列の順番を調べる処理をプログラムにしてみよう
言語は何にするのよ？
あー、なるべくいろんな言語で書きたいところだね～
例えば
Malbolge 最強に難しいプログラムを作ろうということで
開発された、コンセプトの段階でどうしようもない言語
ただ、最近はある程度思い通りにかけるという話も
詳細は全くわかりませんが
とか？
なんてもんやらせようとしてるのよ
ゆる して にゃん♪
……
あっ、えーっととりあえずjavascriptあたりで組んでみようかな
今後知っといて損はない言語だから
まあ、大事なのはアルゴリズムだからね
じゃあまず数字を一文字づつ分割するところから始めるとして 
function sequenceNumber = function(value) {
  var valueList = String(value).split('');

}
まず、合計の値を入れる変数を作る
そんで、桁数分だけ繰り返すfor文を作るよ
まあバンバン書いてくよ 
var sequenceNumber = function(value) {
  // 渡された数値を配列にしたもの
  var valueList = String(value).split('');
  // 順番（戻り値）
  var resultValue;

  for (var i = 0; i < valueList.length; i++) {
    // TODO
  }

  return resultValue;
}
そんで、各桁の前の桁を調べるためにもう一個for文をつくる
なんか上手い説明文思いつかないけど、とりあえずこんなかんじ 
var sequenceNumber = function(value) {
  
  // 渡された順列を配列にしたもの
  var valueList = String(value).split('');
  // 順番（戻り値）
  var resultValue;
  
  // 調べたい順列の桁数分だけ繰り返す
  for (var i = 0; i < valueList.lenght; i++) {
    
    // 調べたい桁の数字を抜き出す
    var nowValue = valueList[i];
    
    // 現在調べている桁から前の方を調べる
    for (var j = i; j >= 0; j--) {
      // TODO
    }
  }

  return resultValue;
}
それで、二個目のループの中に「自分の数字より小さい数をかぞえる処理」を入れればいいのね？ 
var sequenceNumber = function(value) {
  
  // 渡された順列を配列にしたもの
  var valueList = String(value).split('');
  // 順番（戻り値）
  var resultValue = 0;
  // 調べたい順列の桁数分だけ繰り返す
  for (var i = 0; i < valueList.length; i++) {
    // 調べてる桁の数字を抜き出す変数
    var nowValue = valueList[i];
    // 調べてる桁の数字より小さい数を数える変数
    var smallCount = 0;
    
    // 現在調べている桁から前の方を調べる
    for (var j = i; j >= 0; j--) {
      // 調べてる桁の数字より小さい数をカウント
      if (valueList[j] < nowValue) {
        smallCount++;
      }
    }
    
    resultValue += (nowValue - smallCount) * fact「階乗の関数」(valueList.length - (i + 1));
  }

  return resultValue;
};
二重ループ最高や！！再帰なんて最初からいらんかったんや！！
あ、
階乗の関数 話の本筋ではないので本文では省略しました（次で使わなくなる予定ですし）
function fact(val){
  var returnVal = 1;
  for(var i = val; i > 0; i--) {
    returnVal *= i;
  }
  return returnVal;
}
必要最低限な処理のみ記述してあります
は適当になんとかしてね

上のテキストボックスに順列を入力すると下のテキストに順番が出力されます
例として5桁の場合、01234をそれぞれ一つずつ入れることで順列の順番が出力されます
数字が重複している場合や数字ではない場合の動作は保証しません
（詰めが雑ね……）
処理ができたのはいいんだけど、じゃあこの小話のタイトル「階乗進数」ってなんなの？
そらもうあれよ、さっき行ったこの数よ
これで言ったら「3211」 
3×4!＋2×3!＋1×2!＋1×1!
んー……？
例えば十進数なら三万二千百四十はこう書くよね？
「32140」
で、これを位ごとに書くとこうなる 
3×104＋2×103＋1×102＋4×101＋0×100
こんな感じで、十進数は10の累乗の
級数 上記のように、並べられた数字を足し算したやつのことを級数といいます
で表される数のこと
おんなじように、自然数の階乗の級数で表される数のことを階乗進数って言うよ
で、これを表す方式を階乗進法っていう
階乗進数を使えば順列の順番がわかるのね
なかなか
便利 ……つい勢いで便利って言っちゃったけど
これ以外にどこで使うの？
ね
というわけで今回はここまでにしようね
またね～